你的递归，真的是递归吗？

after Abelson and Sussman (2002)

factorial(n)的递归表达

相信大家对递归（recursion）概念应该不会陌生。阶乘（factorial）通常是我们学习递归的“入门仪式”：

def factorial(n):
    if n == 1:
        return 1
    return n * factorial(n - 1)

这里实际上是对阶乘递推关系式（$n! = n \times (n-1)!$) 的直接 Python 描述。

让我们跟踪下 factorial(6) 的计算过程：

factorial(6)
6 * factorial(5) // expanding
6 * (5 * factorial(4))
6 * (5 * (4 * factorial(3)))
6 * (5 * (4 * (3 * factorial(2))))
6 * (5 * (4 * (3 * (2 * factorial(1)))))
6 * (5 * (4 * (3 * (2 * 1)))) // contracting
6 * (5 * (4 * (3 * 2)))
6 * (5 * (4 * 6))
6 * (5 * 24)
6 * 120
720

可以看出，整个计算过程形成了一个“先展开（expansion），后收缩（Contraction）“的形状。

1. 展开阶段 (Expansion)：为了计算 factorial(6)，必须先计算 factorial(5)，但不能忘记“等会儿要乘以 6”。这个“待办的乘法”是一个延迟操作（deferred operation）。随着递归深入，延迟操作链不断变长，计算机需要用内存（通常是调用栈（call stack））记住每一层的待办事项。
2. 收缩阶段 (Contraction)：当递归触底（n == 1 返回 1），这些延迟操作才开始逐一执行，完成计算。

可以看出，这个过程的关键是“记忆“。计算机必须使用栈来记住这一长串的待办事项。当 $n$ 很大时，需要记住的东西也线性增加。也就是说，计算机需要跟踪的信息随着 $n$ 线性增长。这一过程也被称为线性递归过程（Linear recursive process），其内存消耗为 $O(n)$。

factorial(n)的迭代表达

除了以上从递推式的方式求解阶乘外，我们还可以从另外一个视角来计算整数的阶乘。

def fact_iter(product, counter, max_count):
    if counter > max_count:
        return product
    return fact_iter(product * counter, counter + 1, max_count)

def factorial(n):
    return fact_iter(1, 1, n)

该程序计算整数阶乘的思路是：首先将 1 乘以 2， 然后将其结果乘以 3， 再乘以 4， 如此继续，直到我们乘到 $n$ 为止。也就是说，该段程序本质上是在执行：$1 \times 2 \times 3 \ldots \times n = n!$。为此，这里需要维护一个乘积变量（product）以及一个从 1 增长到 $n$ 的计数器 (counter)，并且规定当计数器的值超过 $n$ 时的乘积值就是 $n!$ 的结果。

同样，我们来跟踪下新的 factorial(6) 的计算过程：

factorial(6)
fact_iter(1, 1, 6)
fact_ter(1, 2, 6)
fact_iter(2, 3, 6)
fact_iter(6, 4, 6)
fact_iter(24, 5, 6)
fact_iter(120, 6, 6)
fact_iter(720, 7, 6)

观察这个过程，可以发现与前面的有着本质区别：

1. 没有延迟操作：在每次调用fact_iter 自身之前，所有必要的计算（如 product * counter）都已经完成计算了。
2. 状态完全有参数捕获： 在任何时候，我们只需要知道 product，counter，max-count 这三个状态变量的值，就能完整描述计算的状态。计算机不再需要“记住”任何格外的东西。
3. 过程形状时平的：它没有“展开-收缩”的阶段，只是平稳的从一个状态过渡到下一个状态，直到终点。它消耗的内存时恒定的，也即$O(1)$。

这种行为其实和一个简单的循环是完全一样的。因此，也被称为迭代过程（Iterative process）

def factorial(n):
    """
    Equivalent iterative implementation using explicit loop.
    This shows the same logic without recursion.
    """
    product = 1
    counter = 1
    while counter <= n:
        product *= counter
        counter += 1
    return product

结论

从 factorial(n) 的两种实现来看，一个使用了递归语法的程序（procedure），并不一定会产生一个递归形状的过程（process）。

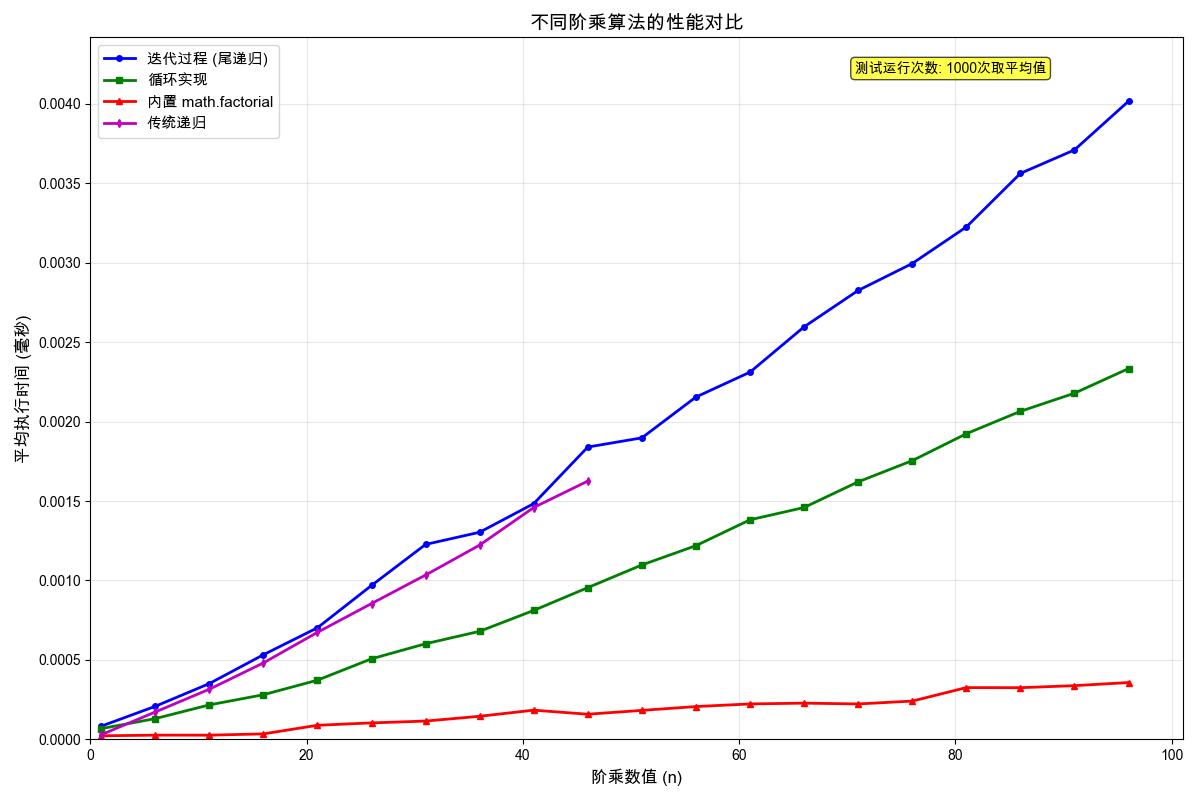
练习

def inc(x):
    return x + 1

def dec(x):
    return x - 1

def add_v1(a, b):
    if a == 0:
        return b
    return inc(add_v1(dec(a), b))

def add_v2(a, b):
    if (a == 0):
        return b
    return add_v2(dec(a), inc(b))

请分析 add_v1(4, 5) 和 add_v2(4, 5)的求值过程，判断每个函数生成的计算过程是迭代（Iterative）还是递归（Recursive）。

参考答案

Reference

Abelson, H., Sussman, G.J., 2002. Structure and Interpretation of Computer Programs, 2nd ed. MIT Press.