由于内容偏多,我将《基于回归算法预测股市价格》实验项目拆分成了多篇文章。这是该系列的第 三 篇文章!这里主要介绍线性回归模型的训练过程等内容。
相关文章链接:
- 第一篇:基于回归算法预测股市价格(Part 1)
- 第二篇:基于回归算法预测股市价格(Part 2)
- 第三篇:基于回归算法预测股市价格(Part 3: Estimating with Linear Regression)(正在阅读)
- 第四篇:基于回归算法预测股市价格(Part 4: Estimating with Tree-based Regression)
- 第五篇:基于回归算法预测股市价格(Part 5: Estimating with Network-based Regression)
以下回归算法均使用 scikit-learn 包。
Implementing Linear Regression with LinearRegression
下面这段代码展示了一个一般性的回归模型的构建、超参数调优以及最终的模型评估的过程,这里以线性回归为例说明其具体步骤如下:
首先,导入了必要的库,包括 sklearn.linear_model 的 LinearRegression 进行回归建模,sklearn.metrics 用于计算模型的评估指标,sklearn.model_selection 的 GridSearchCV 用于执行超参数搜索,sklearn.pipeline 的 Pipeline 用于构建数据处理与建模的流水线,sklearn.preprocessing 的 StandardScaler 用于数据标准化。
接下来,定义了一个 Pipeline,其中包含两个步骤:首先使用 StandardScaler 对数据进行标准化,以确保特征具有相似的尺度,避免数值范围不同对模型造成影响;然后应用 LinearRegression 进行回归建模。
随后,定义了一个超参数搜索网格 param_grid,其中只包含 LinearRegression 的 fit_intercept 参数,该参数决定是否在回归模型中使用截距项。由于 LinearRegression 本身的可调参数较少,这里仅对 fit_intercept 进行了优化(作为 Demonstration)。
在第 3 部分中,为了寻找最佳的超参数组合,我们使用 GridSearchCV 进行超参数搜索,其中采用 3 折交叉验证(cv=TimeSeriesSplit(n_splits=3)),并使用 负均方误差(Negative Mean Squared Error,MSE) 作为评分标准(scoring='neg_mean_squared_error')。这意味着在交叉验证过程中,模型会在不同的数据子集上进行训练和验证,并基于均方误差选择最优参数组合。n_jobs=-1 允许并行计算(parallel computing),以提高搜索效率。然后,grid_search.fit(X_train_transformed, y_train_aligned) 通过训练数据进行拟合,寻找最佳超参数。
一旦超参数搜索完成,通过 print 函数打印出 grid_search.best_params_,即在交叉验证过程中找到的最优超参数。
最后,在测试集( X_test_transformed)上评估最终的模型,并计算同样的评估指标(MSE、RMSE、$R^2$)。这样可以衡量模型在真正未知数据上的泛化能力。
第 6 部分以表格形式格式化输出了 测试集 的评估指标,便于直观比较模型的性能。咱们可以根据这些指标判断模型是否在测试集上都表现良好,或者是否出现了过拟合或欠拟合的问题。
总的来说,这是一段比较完整的机器学习建模流程,包括数据预处理、模型构建、超参数调优、交叉验证以及最终的性能评估。如果需要其他模型,比如后面选择了 SGDRegressor,我们只需要通过类似的方式引入 SGDRegressor 类,然后重新设置相应的流水线以及用于搜索网格的超参数就可以了。
from balabs.regression.models.model_evaluation import evaluate_model
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import GridSearchCV, TimeSeriesSplit
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# X_train_transformed, y_train_aligned, X_test_transformed, y_test_aligned have been obtained
# from the previous data splitting and feature engineering steps, only droping original columns except 'Open'.
# Build a pipeline with a StandardScaler and a LinearRegression model
pipeline = Pipeline(
[("scaler", StandardScaler()), ("linearregression", LinearRegression())]
)
# Define a parameter grid for hyperparameter tuning
# Here, we only tune the 'fit_intercept' parameter as an example (LinearRegression does not have many hyperparameters)
param_grid = {"linearregression__fit_intercept": [True, False]}
# Initialize GridSearchCV with cross-validation using negative MSE as the scoring metric
tscv = TimeSeriesSplit(n_splits=3)
grid_search = GridSearchCV(
pipeline, param_grid, cv=tscv, scoring="neg_mean_squared_error", n_jobs=-1
)
grid_search.fit(X_train_transformed, y_train_aligned)
best_model = grid_search.best_estimator_
# Print the best hyperparameters
print("Best parameters: ", grid_search.best_params_)
# Evaluate the model on test sets
test_metrics = evaluate_model(best_model, X_test_transformed, y_test_aligned, "Test")
结果为:
Best parameters: {'linearregression__fit_intercept': True}
Test Set Performance:
================================================================================
Metric Value Unit
--------------------------------------------------------------------------------
Mean Squared Error (MSE) 7.2971e-01
Root MSE (RMSE) 0.8542 Price Units
Mean Absolute Error (MAE) 0.6464 Price Units
Mean Abs Percentage Error (MAPE) 0.45 %
R-squared (R2) 0.9987
Directional Accuracy 80.13 %
在本次模型评估中,我们得到的最优参数是 {'linearregression__fit_intercept': True},这意味着在模型训练过程中保留了截距项,而不是强制回归通过原点。从测试集的评估指标来看,线性回归模型表现得异常优秀,其均方误差(MSE)仅为 0.73,均方根误差(RMSE)低至 0.85,R^2 高达 0.9987,方向性准确率为 80.13%。这意味着模型几乎能够完美预测测试集中的目标变量。然而,在金融市场预测的背景下,这种近乎“无懈可击”的表现实际上是一个危险信号,值得深入探讨其中的潜在问题。
首先,高 R^2 可能是由于特征间的高度共线性。在此前的方差膨胀因子(VIF)分析中,我们发现 35 个特征中,只有 7 个特征满足 VIF < 5 的标准,这意味着大多数特征之间存在严重的多重共线性。多重共线性会导致模型的回归系数变得不稳定,使得模型在训练数据上表现优异,但在真实环境中很可能难以泛化。尤其是在股票市场预测中,许多技术指标(如均线、动量指标、成交量指标等)往往是目标变量的某种变换形式,保留过多冗余信息的特征,可能使模型仅仅是在“复制”历史价格,而不是学习市场的真实规律。
另一个值得关注的问题是数据泄露的风险。如果特征构造过程中无意间使用了未来的信息,模型可能会在训练阶段“看到”它本不应该掌握的数据,从而导致测试集上的极佳表现,但在真实预测中完全失效。例如,如果某些滞后变量(如 Close_t-1、MA_5 等)在构造过程中未严格遵循时间序列的顺序,或者在数据划分时未来数据混入了训练集,那么模型实际上是被“作弊训练”出来的。尽管去除了部分原始数据列,如 Close、Volume 等,但仍需检查技术指标、滞后变量的构造过程,确保测试集严格按照时间先后顺序进行预测,而非回溯过去数据。
此外,特征冗余也可能导致过拟合。在特征相关性分析中,我们发现 23 个特征的绝对相关系数大于 0.1,其中一些甚至接近 1。例如,High、Low、Open、Close_t-1、MA_5、EMA_12 等特征与目标变量高度相关,这可能意味着模型的预测结果主要依赖于这些强相关变量,而不是捕捉市场的动态变化。如果某些变量仅仅是目标变量的线性变换或者简单滞后,而没有引入真正的市场驱动因素(如资金流向、宏观经济数据、市场情绪等),那么模型虽然能够在短期内做出精准预测,但缺乏实际的决策价值。
从改进方向来看,减少共线性特征并优化特征选择是提升模型稳健性的关键。可以减少高 VIF 的变量,优先保留 VIF 较低的特征,以降低共线性对模型的影响。也可以引入递归特征消除(RFE)或 Lasso 正则化,以自动筛选最具解释力的特征,而非盲目保留所有变量。此外,通过主成分分析(PCA) 进行降维,也可以减少冗余信息对模型的干扰,提高泛化能力。在时间序列建模方面,还可以采用 滚动窗口交叉验证 或 扩展窗口交叉验证,以确保训练和测试数据之间的时间一致性,从而避免潜在的信息泄露问题。
值得一提的是,线性模型可能并非市场预测的最佳选择。虽然其结果直观且易于解释,但面对非线性、非平稳的金融市场数据,其表现往往受到诸多限制。因此,引入非线性模型(如随机森林、XGBoost、LSTM 神经网络等)可能是更为合理的方案,这些模型能够捕捉复杂的市场动态,同时避免线性回归的局限性。与此同时,加入正则化方法,比如 Ridge,可以有效防止模型依赖某些特定变量,从而增强其稳定性和抗干扰能力。
总结来看,当前的回归结果尽管在测试集上表现完美,但更可能是受到共线性、数据泄露、特征冗余等问题的影响。为了确保模型具备真正的预测能力,而非仅仅在历史数据上回溯过去,需要进一步优化特征选择、强化时间序列处理方式,并考虑引入更具鲁棒性的非线性模型。市场预测的目标不仅仅是提升历史数据上的准确性,更重要的是在真实市场环境中具备可行性和稳定性。
Reducing High VIF Features
# Get the VIF values of the features
vif = feature_gen.get_vif(X_train_transformed, threshold=10).set_index("Feature")
# Drop the features with high VIF values
X_train_filtered = X_train_transformed.loc[:, vif.index]
X_test_filtered = X_test_transformed.loc[:, vif.index]
这里,将计算 VIF 的阈值设置为 10,并提取满足 VIF <= 10 的特征。然后将其作为 grid_search.fit的输入,并计算训练后的模型在测试集上的评分。结果如下:
Best parameters: {'linearregression__fit_intercept': True}
Test Set Performance:
================================================================================
Metric Value Unit
--------------------------------------------------------------------------------
Mean Squared Error (MSE) 4.6846e+03
Root MSE (RMSE) 68.4438 Price Units
Mean Absolute Error (MAE) 61.9964 Price Units
Mean Abs Percentage Error (MAPE) 41.16 %
R-squared (R2) -7.3400
Directional Accuracy 52.53 %
从模型的评估结果来看,在去除了 VIF 过高的特征后,模型的性能发生了显著变化。比如说,MSE 和 RMSE 显著上升:均方误差 (MSE) 从接近 0 变为 4684.6,均方根误差 (RMSE) 也增长至 68.44。这表明模型不再能够完美拟合测试数据,而是存在一定的误差,这在一定程度上说明之前的模型可能确实存在过度拟合的问题。MAE 和 MAPE 也明显增加:平均绝对误差 (MAE) 增长到 61.99,而平均绝对百分比误差 (MAPE) 也达到了 41.16%。这说明模型在绝对值误差和相对误差方面都变得较大,预测精度下降。这可能是由于删除了 VIF 过高的特征后,模型丧失了部分与目标变量高度相关的信息,导致误差变大。
R^2 甚至变为负值 (-7.34),这表明模型的预测能力非常差,甚至不如简单的均值预测。理论上,R^2 的值应当在 0 到 1 之间,但当它变为负值时,说明模型的预测误差比直接用均值预测的误差还要大。这是一个很强的信号,表明当前的特征选择方案可能过于激进,导致模型缺乏足够的信息来有效建模目标变量。
方向性准确率(Directional Accuracy)此时也降至 52.53%。方向性准确率衡量了模型对价格上涨或下跌方向的预测是否正确。在随机猜测的情况下,这个值应当接近 50%。当前模型的方向性准确率仅为 52.53%,表明它对市场方向的判断几乎是随机的,说明它缺乏有意义的预测能力。
综合来看,在去除了高 VIF 的特征后,虽然缓解了共线性问题,但也可能丢失了对目标变量非常重要的信息,导致模型的预测能力大幅下降。这说明并不是所有高 VIF 的特征都是“坏的”,有些可能仍然是有价值的,只是它们之间的相关性较高。目前使用的仍然是最基本的 OLS 线性回归模型,但在金融时间序列预测中,市场数据往往存在非线性关系。去除高共线性特征后,模型可能无法捕捉这些非线性关系,导致拟合能力下降。虽然使用了 VIF 筛选特征,但仅仅基于 VIF 进行特征选择可能并不足够,应该结合其他分析,如相关性分析、特征重要性评估(如 Lasso 或树模型的 feature importance)等来更合理地筛选特征。
从这个结果上看,如果仍然使用 OLS 线性回归模型,咱们可以进一步尝试将 VIF 阈值放宽到 15 或 20,以保留部分重要但共线性较高的特征。或者结合特征与目标变量的相关性相关性指标,仅剔除 VIF 高但与目标变量低相关的特征,而保留 VIF 高但目标相关性也高的特征。
Selective Removal of High VIF Variables Based on Target Correlation
high_vif_high_corr_features = feature_gen.get_high_vif_high_corr_features(
X_train_transformed, y_train_aligned, vif_threshold=10.0, corr_threshold=0.1
).set_index("Feature")
X_train_high_vif_high_corr_filtered = X_train_transformed.loc[
:, high_vif_high_corr_features.index
]
X_test_high_vif_high_corr_filtered = X_test_transformed.loc[
:, high_vif_high_corr_features.index
]
🤓 Note
get_high_vif_high_corr_features为定义在FeatureGenerator中的方法,请参考特征工程中的原始代码。
这里提取了 VIF 高但目标相关性也高的特征所有特征,然后将其作为 grid_search.fit的输入,并计算训练后的模型在测试集上的评分。结果如下:
Best parameters: {'linearregression__fit_intercept': True}
Test Set Performance:
================================================================================
Metric Value Unit
--------------------------------------------------------------------------------
Mean Squared Error (MSE) 1.0768e+00
Root MSE (RMSE) 1.0377 Price Units
Mean Absolute Error (MAE) 0.7884 Price Units
Mean Abs Percentage Error (MAPE) 0.55 %
R-squared (R2) 0.9981
Directional Accuracy 80.05 %
从模型评估结果来看,线性回归模型的表现依然非常出色,MSE 仅为 1.08,RMSE 约为 1.04,R^2 达到了 0.9981,方向性准确率为 80.05%。与先前的实验相比,这一结果依然保持了较高的预测精度,同时避免了过度依赖某些高度共线性的变量。对比上节结果,也可以发现,通过针对性地剔除高 VIF 但低相关的特征,我们成功减少了特征冗余带来的问题,同时仍然保留了对目标变量真正重要的信息。
Feature Importance Analysis Using Lasso Regression
Lasso 回归相比普通线性回归多了一个 L1 正则化参数(alpha),其功能是将不重要的特征系数压缩到 0,从而实现自动的特征选择。
from sklearn.linear_model import Lasso
# X_train_transformed, y_train_aligned, X_test_transformed, y_test_aligned have been obtained
# from the previous data splitting and feature engineering steps, only droping original columns except 'Open'.
# Build a pipeline with a StandardScaler and a Lasso model
pipeline = Pipeline([("scaler", StandardScaler()), ("lasso", Lasso())])
# Define a parameter grid for hyperparameter tuning
param_grid = {
"lasso__alpha": [0.001, 0.01, 0.1, 1.0, 10.0],
"lasso__fit_intercept": [True, False],
}
# Initialize GridSearchCV with cross-validation using negative MSE as the scoring metric
tscv = TimeSeriesSplit(n_splits=3)
grid_search = GridSearchCV(
pipeline, param_grid, cv=tscv, scoring="neg_mean_squared_error", n_jobs=-1
)
grid_search.fit(X_train_transformed, y_train_aligned)
best_model = grid_search.best_estimator_
# Print the best hyperparameters
print("Best parameters: ", grid_search.best_params_)
# Evaluate the model on test sets
test_metrics = evaluate_model(best_model, X_test_transformed, y_test_aligned, "Test")
从代码上看,相对于 LinearRegression,这里只是将其换成了 Lasso。然后,针对性得修改了该算法用于网格搜索得参数空间 param_grid。其他保持不变。评估得分如下:
Best parameters: {'lasso__alpha': 0.01, 'lasso__fit_intercept': True}
Test Set Performance:
================================================================================
Metric Value Unit
--------------------------------------------------------------------------------
Mean Squared Error (MSE) 1.1296e+00
Root MSE (RMSE) 1.0628 Price Units
Mean Absolute Error (MAE) 0.7977 Price Units
Mean Abs Percentage Error (MAPE) 0.55 %
R-squared (R2) 0.9980
Directional Accuracy 66.86 %
基于完整的特征工程数据(X_train_transformed)训练,最优参数为 {'lasso__alpha': 0.01, 'lasso__fit_intercept': True}。测试集性能显示:MSE 为 1.13,RMSE 为 1.06,MAE 为 0.80,MAPE 为 0.55%,R^2 为 0.9980,方向性准确率为 66.86%。这些指标表明,模型在测试集上表现出色,尤其是 R^2 高达 0.9980,说明模型几乎完美解释了目标变量的方差。然而,这种近乎完美的表现可能隐藏了一些问题。Lasso 回归通过 L1 正则化(alpha=0.01 表示较弱的正则化)对特征系数进行压缩,但正则化强度较低,可能未完全消除高共线性特征的影响。这种特征冗余和高共线性与基本的线性模型遇到的问题一致,都可能导致模型在训练和测试数据上过度拟合历史模式,而非真正捕捉市场动态。方向性准确率 66.86% 虽高于随机猜测(50%),但在金融预测中仍不算理想,表明模型对价格方向的预测能力有限。
此外,也可以通过如下方式,查看经过Lasso回归后的模型系数:
lasso_coef = best_model.named_steps["lasso"].coef_
feature_names = X_train_transformed.columns
coef_df = pd.DataFrame({"Feature": feature_names, "Coefficient": lasso_coef})
print("Lasso coefficients:\n", coef_df[coef_df["Coefficient"] != 0])
其结果为:
Lasso coefficients:
Feature Coefficient
0 Open 41.601923
4 MonthEnd -0.000362
6 Close_t-1 0.000392
7 Return_t-1 0.661249
8 MA_5 0.008289
13 Gap -0.257378
14 HV_10 -0.009709
19 Vol_Chg -0.000856
20 VPT 0.117049
22 MACD 0.027289
28 GapDir -0.116058
29 GapAbs -0.004028
Feature Importance Analysis Using Ridge Regression
类似 Lasso 回归,只需要修改 Pipeline 和 param_grid
pipeline = Pipeline([
("scaler", StandardScaler()),
("ridge", Ridge())
])
param_grid = {
"ridge__alpha": [0.01, 0.1, 1.0, 10.0, 100.0],
"ridge__fit_intercept": [True, False]
}
评估结果如下:
Best parameters: {'ridge__alpha': 0.01, 'ridge__fit_intercept': True}
Test Set Performance:
================================================================================
Metric Value Unit
--------------------------------------------------------------------------------
Mean Squared Error (MSE) 7.3871e-01
Root MSE (RMSE) 0.8595 Price Units
Mean Absolute Error (MAE) 0.6474 Price Units
Mean Abs Percentage Error (MAPE) 0.45 %
R-squared (R2) 0.9987
Directional Accuracy 78.54 %
Ridge coefficients:
Feature Coefficient
0 Open 41.601923
4 MonthEnd -0.000362
6 Close_t-1 0.000392
7 Return_t-1 0.661249
8 MA_5 0.008289
13 Gap -0.257378
14 HV_10 -0.009709
19 Vol_Chg -0.000856
20 VPT 0.117049
22 MACD 0.027289
28 GapDir -0.116058
29 GapAbs -0.004028
Evaluating Feature Importance with Shapley Values
Shapley 值最早源于博弈论,是一种用于衡量各个参与者在合作博弈中的公平贡献的方法。在机器学习中,咱们可以把模型预测看作一个合作博弈,每个特征(Feature) 都是一个“玩家”,而最终的预测结果是这些玩家共同作用的产物。Shapley 值的目标就是衡量每个特征对模型预测的贡献大小,以此作为解释模型决策的依据。比如说,可以借助于shap 包的的 .force_plot 画出一个力场图,在这个图中:
- 基准值(Base Value) 代表模型的全局平均预测值,相当于默认情况下模型的期望输出。
- 每个特征的 SHAP 贡献值 可以是 正向(红色) 或 负向(蓝色),分别表示该特征增加或减少了最终的预测值。
通过这些信息,我们能够直观地理解某个预测结果是如何形成的,进而提高模型的透明度和可信度。
除了个别样本,我们还可以使用 Shapley 值的均值来衡量模型整体的特征重要性。这种方法可以帮助我们识别哪些特征对模型决策影响最大。常见的可视化方法包括:
shap.summary_plot(散点图),该图可以展示不同特征的 Shapley 值分布,分析特征对预测值的影响方向。- 可以在
shap.summary_plot方法中指定plot_type = bar画出对应的柱状图,以此展示所有样本上的 Shapley 值均值,从而衡量特征的重要性排序。
从这些图表中,我们可以发现某些特征对预测结果有着显著影响,而另一些特征几乎没有贡献。通过这样的分析,我们可以对模型进行特征选择,移除低价值特征,提高模型的可解释性和计算效率。
下面是在最基本的 LinearRegression 模型的基础上展示如何计算和可视化 Shapley 值的过程。
import shap
# X_train_transformed, y_train_aligned, X_test_transformed, y_test_aligned have been obtained
# from the previous data splitting and feature engineering steps, only droping original columns except 'Open'.
# Build and train the pipeline
pipeline = Pipeline(
[("scaler", StandardScaler()), ("linearregression", LinearRegression())]
)
param_grid = {"linearregression__fit_intercept": [True, False]}
tscv = TimeSeriesSplit(n_splits=3)
grid_search = GridSearchCV(
pipeline, param_grid, cv=tscv, scoring="neg_mean_squared_error", n_jobs=-1
)
grid_search.fit(X_train_transformed, y_train_aligned)
best_model = grid_search.best_estimator_
print("Best parameters: ", grid_search.best_params_)
# Evaluate the model (assuming evaluate_model is defined)
test_metrics = evaluate_model(best_model, X_test_transformed, y_test_aligned, "Test")
# Extract the linear regression model
linear_model = best_model.named_steps["linearregression"]
# Prepare scaled test data
X_test_scaled = best_model.named_steps["scaler"].transform(X_test_transformed)
# Create SHAP explainer
explainer = shap.LinearExplainer(linear_model, X_train_transformed)
# Compute SHAP values
shap_values = explainer.shap_values(X_test_scaled)
# Visualize SHAP values
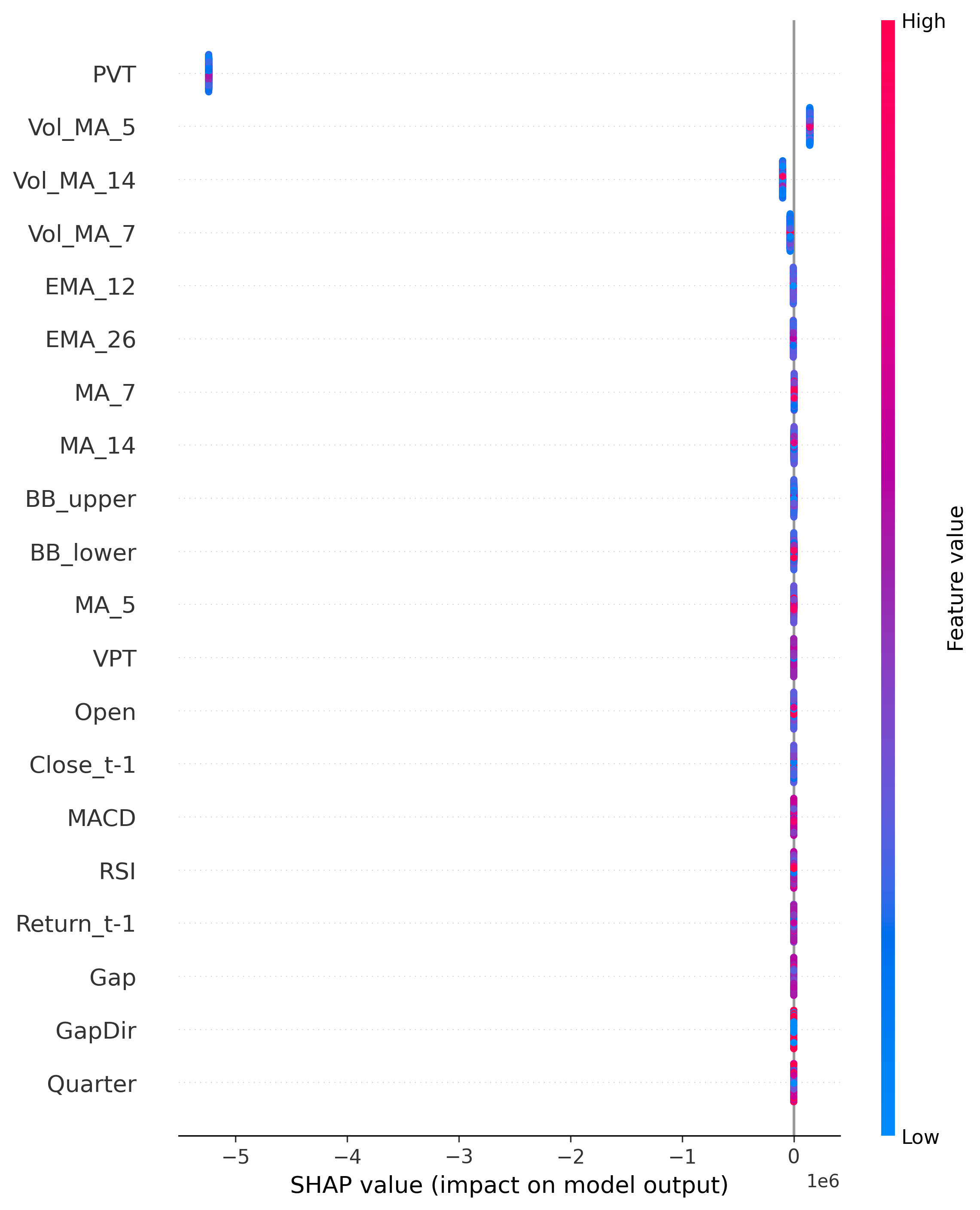
shap.summary_plot(shap_values, X_test_transformed, feature_names=X_test_transformed.columns) # Summary plot
shap.summary_plot(shap_values, X_test_transformed, plot_type="bar", feature_names=X_test_transformed.columns) # Bar plot
shap.force_plot(explainer.expected_value, shap_values[0], X_test_transformed.iloc[0], feature_names=X_test_transformed.columns) # Force plot
结果如下:
Summary plot
Bar plot

Force plot
